Лекция 15. Графы
4.3. Деревья и лес
Свойства деревьев
Определение 4.12. ГрафВершину графа, инцидентную только одному его ребру, называют концевой (или висячей) вершиной, а ребро, инцидентное концевой вершине, будем называть концевым ребром графа.
Среди различных деревьев выделяют два важных частных случая: последовательное дерево, представляющее собой простую цепь, и звездное дерево (или куст), в котором одна из вершин (центр) смежна со всеми остальными вершинами. Пусть множество ![]() содержит
содержит ![]() вершин. Связав эти вершины
ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее
данное множество вершин. Для двух вершин существует одно покрывающее дерево
- сами вершины и ребро, их связывающее. С увеличением
вершин. Связав эти вершины
ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее
данное множество вершин. Для двух вершин существует одно покрывающее дерево
- сами вершины и ребро, их связывающее. С увеличением
![]() число различных
деревьев
число различных
деревьев ![]() быстро
увеличивается:
быстро
увеличивается:
![]() .
.

Среди графов n-го порядка (с n вершинами) без кратных ребер полный граф имеет наибольшее количество ребер, а дерево (n-го порядка) - наименьшее. Дерево содержит минимальное количество ребер, необходимое для того, чтобы граф был связным.
Теорема 4.9. Каждое
дерево с ![]() вершинами
имеет в точности
вершинами
имеет в точности ![]() ребро.
ребро.
Нетрудно убедиться в справедливости следующих теорем.
Теорема 4.10. Граф является деревом тогда и только тогда, когда каждая пара различных вершин графа соединяется одной и только одной простой цепью.
Теорема 4.11. У каждого дерева найдется висячая вершина.
Теорема 4.12. При удалении любого ребра дерева оно распадается на связные компоненты, являющиеся либо изолированными вершинами, либо деревьями. При добавлении в дерево любого нового ребра в нем образуется простой цикл, и оно перестает быть деревом.
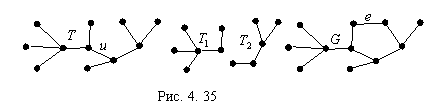
Дерево на рис. 4. 35 при
удалении ребра ![]() распадается
на лес из двух деревьев
распадается
на лес из двух деревьев ![]() и
и ![]() , а после добавления ребра
, а после добавления ребра ![]() превращается в циклический
граф
превращается в циклический
граф ![]() .
.
Рассматриваются также
деревья с ориентированными ребрами (дугами). Ориентированное дерево называется
прадеревом с корнем ![]() ,
если существует простой путь между вершиной
,
если существует простой путь между вершиной ![]() и любой
и любой
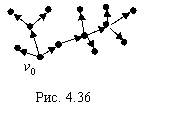
другой его вершиной (рис. 4.36). Прадерево может иметь только один корень.
Типы вершин дерева и его центры
Рассмотрим
дерево ![]() с
с
![]() вершинами. Назовем его
концевые вершины вершинами типа 1. Теперь удалим все вершины типа
1 и концевые ребра. В результате получим связный граф без циклов
вершинами. Назовем его
концевые вершины вершинами типа 1. Теперь удалим все вершины типа
1 и концевые ребра. В результате получим связный граф без циклов ![]() , то есть опять дерево,
но с уже меньшим количеством вершин. Концевые вершины дерева
, то есть опять дерево,
но с уже меньшим количеством вершин. Концевые вершины дерева ![]() назовем вершинами типа
2 в дереве
назовем вершинами типа
2 в дереве ![]() .
Аналогично определяются вершины типов 3, 4 и т. д. Легко видеть, что дерево
может иметь либо одну вершину максимального типа, либо две таких вершины.
Типы вершин дерева
.
Аналогично определяются вершины типов 3, 4 и т. д. Легко видеть, что дерево
может иметь либо одну вершину максимального типа, либо две таких вершины.
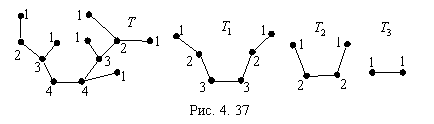
Типы вершин дерева ![]() ,
изображенного на рис. 4. 37, записаны рядом
с соответствующими вершинами. Здесь же показаны последовательные этапы процедуры,
позволяющей их определить. Это дерево имеет две вершины максимального типа.
Если у дерева
,
изображенного на рис. 4. 37, записаны рядом
с соответствующими вершинами. Здесь же показаны последовательные этапы процедуры,
позволяющей их определить. Это дерево имеет две вершины максимального типа.
Если у дерева ![]() удалить
одну из вершин типа 2 и ребра, ей инцидентные, то получившееся при этом
дерево будет иметь уже только одну вершину максимального типа.
удалить
одну из вершин типа 2 и ребра, ей инцидентные, то получившееся при этом
дерево будет иметь уже только одну вершину максимального типа.