|
Моей матери Клавдии Александровне Клюшниковой посвящаю |
ПРЕДИСЛОВИЕ
Вопрос об устойчивости конструкций имеет давнюю и богатую историю. Начало было положено в середине восемнадцатого века работами Эйлера, и заложенная им в основу исследования концепция (эйлеров критерий устойчивости) просуществовала без изменений вплоть до нашего века. Затем было обнаружено, что эта концепция имеет ограниченную область применения даже для упругих систем, а для неупругих — вообще приводит к неправильным результатам. Последнее обстоятельство, выявленное в середине сороковых годов, оказалось переломным в истории развития теории устойчивости деформируемых систем. Интерес к проблеме устойчивости из прикладной области переместился в область физико-математических ее основ и вызвал появление различных новых концепций, ориентированных на применение к конструкциям с данными механическими свойствами (пластичность, ползучесть, наследственность и т. д.). Такая разобщенность теории, просматривающаяся и в современной учебной литературе по устойчивости деформируемых систем, естественно, мешает цельному, а в связи с ограниченностью набора концепций и правильному восприятию предмета.
В данной книге используется единый подход к изучаемой проблеме, основанный на выделении множества особых точек процесса деформирования разного порядка и разной природы, имеющих то или иное отношение к устойчивости. Предлагаются также единый способ вывода разрешающих уравнений для различных конструкций (от стержня до пространственного тела) и единый метод их решения для различных сред сведением к задаче для некоторой линейно-упругой среды.
Книга включает исследования по устойчивости стержней, пластинок, цилиндрических оболочек и пространственных тел для упругих, пластических, линейно-вязких, нелинейно-вязких (ползущих) и наследственных сред. Исходным материалом для ее написания послужили лекции по устойчивости деформируемых систем, читаемые автором на механико-математическом факультете Московского университета.
Автор приносит благодарность Л. Г. Попову за ценные замечания по тексту рукописи, То Ван Тану за обработку экспериментальных данных, а также И. В. Задорожко, М. А. Гамрат-Курек и С. Н. Подзорову за помощь при оформлении рукописи.
Глава IВведение.
КРИТЕРИИ УСТОЙЧИВОСТИ
Прежде чем приступить к изучению явления неустойчивости- в реальных конструкциях, давать общие формулировки и строить методы решения конкретных задач, полезно и важно разобраться в принципиальной стороне дела на примерах моделей, способных, с одной стороны, воспроизводить явления неустойчивости, а с другой - допускать максимально простое математическое описание происходящих процессов. Труд, затраченный на такие исследования, окупается тем, что возникают хотя, может быть, и разрозненные, но предельно ясные картины поведения систем при потере устойчивости, выявляются главные характеристики, ответственные за неустойчивость, что в целом помогает формировать подход к решению проблемы для реальных конструкций.
§ 1. МОДЕЛЬ СТЕРЖНЯ
Прямой центрально сжатый стержень постоянного сечения (рис. 1,а) представляет собой простейшую реальную конструкцию, способную при определенных условиях потерять устойчивость, видимым проявлением чего является выпучивание, т.е. возникновение бокового смещения, не требующего приложения поперечных сил. Долгое время этот объект служил иллюстратором основных сторон явления неустойчивости в деформируемых системах, пока не возникла необходимость разобраться в явлении выпучивания деформируемых систем, материал которых является сложной средой и не подчиняется закону упругости. Оказалось, что уже для упруго-пластического материала, если не навязывать стержню определенный тип поведения, математическое описание явления становится столь сложным, что иллюстративные качества этого объекта утрачиваются полностью и приходится искать более простой объект.
В некоторых случаях приемлемым для выявления принципиальной стороны явления может служить идеализированный двутавр, т. е. стержень из двух параллельных тонких полок, соединенных перемычкой, работающей лишь на сдвиг. Но и этот объeкт для той же пластичности, например, оказывается слишком сложным, и приходится идти на дальнейшие упрощения. Таким образом, возникает простейшая модель стержня, иногда называемая моделью Шенли, которая состоит из двух абсолютно жестких рычагов, соединенных двумя короткими и тонкими полками из исследуемого материала (короткий кусок идеализированного двутавра) (рис. 1,6). Именно эта модель будет положена в основу исследования данной главы, в связи с чем для нее требуется детализировать кинематическую и силовую картину.
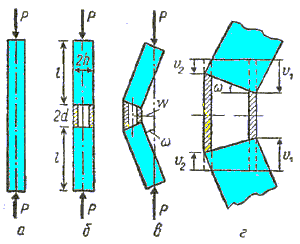
Будем обозначать длины жестких рычагов через l, расстояние между полками 2h, их длины 2d, причем h, d << l, площади поперечного сечения полок одикаковы и равны F/2. Полки должны работать лишь на растяжение-сжатие, так что форма выпучивания (рис. 1,е) полностью определяется углом w и средней деформацией полок е. Если приписать правой полке индекс 1, а левой - 2, то при условии малости деформаций и угла поворота со будем, очевидно, иметь
| (1.1) |
|
| (1.2) |
где Р - внешняя сжимающая сила, М - внешний изгибающий момент. Здесь полезно отметить, что именно последняя из формул (1.2) отличает данную постановку от так называемой геометрически линейной, в которой нужно было бы положить М = 0, т.е. при составлении уравнений статики не учитывать изменения геометрии конструкции. При такой постановке, как правило, справедлива теорема единственности, и поэтому, как будет ясно из дальнейшего, описать явление выпучивания невозможно. Геометрически линейная постановка слишком упрощена, и в вопросах устойчивости от нее приходится отказаться.
При введении обозначений
| (1.3) |
| (1.4) |