Способ 3. Одним из методов
искусственного
интеллекта
является муравьиный
алгоритм Марко Дориго1. Основная идея
алгоритма подсмотрена в природе и имитирует движение
колонии муравьев. По форме этот алгоритм похож на жадный
Nva (способ 1) и в некоторой степени является его
обобщением. Если в алгоритме ближайшего соседа выбор
дальнейшего пути производится, исходя из минимального
расстояния до очередной вершины, то здесь выбором управляет
случайная функция, направляющая движение от текущего
положения с большей вероятностью в вершину j, в которой
наибольшее значение некоторой функции Pij,k (где i
- номер вершины, в которой производится выбор, k - номер
муравья, движущегося по дугам графа). Как и в Nva, во время
движения создается список пройденных вершин, что позволяет
избежать преждевременного зацикливания. Приведем вид
функции, управляющей переходом из данной вершины i в
вершину j:
где tij - количество
феромона (pheromon), оставленного муравьями
на дуге [i,j]; hij - величина, обратная весу
(длине) дуги [i,j]; a, b - эмпирические
коэффициенты. Функция Pij,k подсказывает муравью номер
вершины j, в которую он должен направиться. В знаменателе
(1) стоит нормирующий коэффициент, такой, что 0 Ј Pij,k Ј 1. Индекс m в сумме пробегает по всем
непройденным вершинам, смежным с i. В реальности муравей
оставляет след (феромон) во время прохождения пути, и чем
чаще он возвращается в исходную точку (а это возможно, если
он выбирает оптимальные пути), тем четче след. В
математической же модели функция tij увеличивается
только по завершении маршрута на величину, обратно
пропорциональную длине маршрута.
При a = 0 алгоритм
совпадает с Nva
- муравей руководствуется только длиной пути.
При b = 0 основой для выбора пути является только опыт
(количество феромона, или <<глубина следа>>) предыдущих
муравьев-исследователей. Важно отметить еще одно отличие от
алгоритма Nva. Выбор пути производится не по максимуму
функции Pij,k, а случайным образом, но на случай,
конечно, влияет значение Pij,k. Поясним это на
примере. Пусть муравей k подошел к некоторой вершине 8 и
обнаружил, что перед ним 7 возможных путей к семи вершинам
(на уже пройденные он внимания не обращает). Куда идти?
Муравей доверяется случаю. Он <<пускает рулетку>> (рис. 4.). В какой
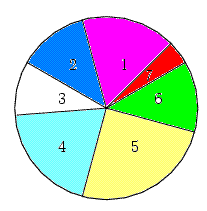
сектор <<шарик>> закатится, туда и идти.
Однако рулетка, размеченная функцией P8 j,k,
j=1,...,7, имеет неравные сектора. Чем ближе вершина и
чем глубже туда след, тем больше сектор. Таким образом,
муравей использует и опыт предшественников (tij), и
здравый смысл (hij ), и случайный фактор, т.е. все
как в жизни.
Для того чтобы не пропустить оптимальное решение, в
муравьином алгоритме предусмотрено <<испарение>> следа. Это
достигается введением коэффициента p в итеративной
формуле tij = (1 - p)tij, применяющейся после
каждого цикла обхода графа.
В алгоритме действует целая колония муравьев. Математически
это означает, что в каждом цикле обхода движение
производится из разных вершин независимым образом.
Здесь приведен самый простой вариант алгоритма. Алгоритм
может быть улучшен. Для ускорения сходимости иногда вводят
так называемых элитных муравьев
[33]. В [7] приведены
наилучшие комбинации параметров a и b.
Bibliography
- [1]
- Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов.
- М.: Мир, 1979.
- [2]
- Асанов М.О., Баранский В.А., Расин В.В.
Дискретная математика: графы, матроиды,
алгоритмы. - Ижевск: НИЦ <<Регулярная и хаотическая
динамика>>, 2001.
- [3]
- Белоусов А.И., Ткачев С.Б. Дискретная математика. - М.: Изд-во МГТУ им. Н.Э. Баумана,
2001.
- [4]
- Берж К. Теория графов и ее применения. - М.: Изд-во иностранной литературы,
1962.
- [5]
- Говорухин В.Н., Цибулин В.Г.
Компьютер в математическом исследовании. Учебный курс. - СПб.: Питер, 2001.
- [6]
- Горбатов В.А., Горбатов А.В., Горбатова М.В.
Дискретная математика. - М.: АСТ, 2003.
- [7]
- Джонс М.Т. Программирование искусственного интеллекта в приложениях. - М.: ДМК Пресс, 2004.
- [8]
- Дьяконов В.П. MAPLE 6: учебный курс. - СПб.: Питер, 2001.
- [9]
- Дьяконов В.П. MATLAB: учебный курс. - СПб.: Питер, 2001.
- [10]
- Емеличев В.А., Мельников О.И., Сарванов В.И.,
Тышкевич Р.И. Лекции по теории графов. - М.: Наука, 1990.
- [11]
- Зубов В.С., Шевченко И.В. Структуры и методы обработки данных. Практикум в среде Delphi.
- М.: Филинъ, 2004.
- [12]
- Иглин С.П. Решение некоторых задач теории графов в MATLAB// Exponenta Pro. Математика в
приложениях. 2004. 4(4).
- [13]
- Иванов Б.Н. Дискретная математика. Алгоритмы и программы.-
М.: Лаборатория базовых знаний, 2002.
- [14]
- Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. - СПб.: БХВ-Петербург, 2003.
- [15]
- Кирсанов М.Н. Решебник. Теоретическая механика/ Под ред. А.И. Кириллова. - М.: Физматлит, 2002.
- [16]
- Кнут Д.Э. Искусство программирования. - М.: Издательский дом <<Вильямс>>, 2003. Т 1, 3.
- [17]
- Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978.
- [18]
- Круг П.Г. Нейронные сети и нейрокомпьютеры. - М.: Изд-во МЭИ, 2002.
- [19]
- Липский В. Комбинаторика для программистов. - М.: Мир, 1988.
- [20]
- Макконнелл Дж. Основы современных алгоритмов. - М.: Техносфера, 2004.
- [21]
- Манзон Б.М. Maple V Power Edition. - М.: ИИД <<Филинъ>>, 1998.
- [22]
- Матросов А. Maple 6. Решение задач высшей математики и механики. - СПб.: БХВ-Петербург,
2001.
- [23]
- Москинова Г.И. Дискретная математика. Математика для менеджера.
- М.: Логос, 2000.
- [24]
- Носов В.А. Комбинаторика и теория графов. - М.: МГУ, 1999.
- [25]
- Оре О. Теория графов. - М.: Наука, 1980.
- [26]
- Очков В.Ф. Mathcad 12 для студентов и инженеров. - СПб.: БХВ-Петербург, 2005.
- [27]
- Показеев В.В., Матяш В.И., Черкесова Г.В., Кирсанов М.Н.
Элементы дискретной математики. Курс лекций. - М.: МГТУ <<МАМИ>>, 2004.
- [28]
- Редькин Н.П. Дискретная математика. - СПб.: <<Лань>>, 2003.
- [29]
- Судоплатов С.В., Овчинникова Е.В. Элементы дискретной
математики. - М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002.
- [30]
- Фляйшнер Г. Эйлеровы графы и смежные вопросы. - М.: Мир, 2002.
- [31]
- Хаггарти Р. Дискретная математика для программистов. - М.: Техносфера, 2003.
- [32]
- Харари Ф. Теория графов. - М.: Едиториал УРСС, 2003.
- [33]
- Штовба С.Д. Муравьиные алгоритмы// Exponenta Pro. Математика в приложениях. 2004. 4(4)
|
