Theorem of the Change in the Kinetic Energy of a System
§ 147. Kinetic Energy of a System
The kinetic energy of a system is defined as a scalar quantity Ò equal to the arithmetical sum of the kinetic energies of all the particles of the system:
Kinetic energy is a characteristic of both the translational and rotational
motion of a system, which is why the theorem of the change in kinetic energy
is so frequently used in problem solutions. The main difference between Ò and
the previously introduced characteristics Q and K0 is that kinetic energy is a
scalar quantity, and essentially a positive one. It, therefore, does not
depend on the directions of the absolute motions of parts of a system and
does not characterise the changes in these directions.
Another important point should be noted. Internal forces act on the parts of
a system in mutually opposite directions. For this reason, as we have seen,
they do not change the vector parameters Q and K0. But if, under the action of
internal forces, the speeds of the particles of a system change, the
quantity Ò will change too. Consequently, the kinetic energy of a system
differs further from the quantities Q and K0 in that it is affected by the action
of both external and internal forces.
If a system consists of several bodies, its kinetic energy is, evidently, equal
to the sum of the kinetic energies of all the bodies:
Let us develop the equations for computing the kinetic energy of a body in
different types of motion.
(1) Translational Motion. In this case all the points of a body
have the same velocity, which is equal to the velocity of the centre of mass.
Therefore, for any point k we have vh = vc, and Eq. (41) gives:
|
Ttrans= |
å
| |
mkvC2
2
|
= |
1
2
|
|
æ
è
|
å
| mk |
ö
ø
|
vC2 |
|
or
Thus, in translational motion, the kinetic energy of a body is equal to half
the product of the body's mass and the square of the velocity of the centre
of mass. The value of Ò does not depend on the direction of motion.
(2) Rotational Motion. The velocity of any point of a body rotating
about an axis Oz (see Fig. 310) is vk=whk, where hk is the
distance of the point from the axis of rotation and ñî is the angular velocity
of the body. Substituting this expression into Eq. (41) and taking the
common multipliers outside of the parentheses, we obtain:
|
Trotation = |
å
| |
mkw2hk2
2
|
= |
1
2
|
|
æ
è
|
å
| mkhk2 |
ö
ø
|
w2. |
|
The term in the parentheses is the moment of inertia of the body with
respect to axis z4. Thus, we finally obtain:
i.e., in rotational motion, the kinetic energy of a body is equal to half
the product of the body's moment of inertia with respect to the axis of
rotation and the square of its angular velocity. The value of Ò does not
depend on the direction of the rotation.
(3) Plane Motion1. In plane motion, the velocities of all the points of a body are at any instant directed as if the body were rotating
about an axis perpendicular to the plane of motion and passing
through the instantaneous centre of zero velocity P (Fig. 316). Hence,
by Eq. (43),
where JP is the moment of inertia of the body with respect to the
instantaneous axis of rotation, and w is the angular velocity of the body.
The quantity JP in Eq. (43') is variable, as the position of the centre
P continuously changes with the motion of the body. Let us introduce instead
of JP a constant moment of inertia Jc with respect to an axis through
the centre of mass C of the body. By the parallel axis theorem (§ 132),
JP = Jc + Md2, where d = PC. Substituting this expression for
JP into Eq. (43') and taking into
account that point P is the instantaneous centre of zero velocity and
therefore wd = wPC = vC, where vc
is the velocity of the centre of mass, we
obtain finally:
|
Tplane = |
1
2
|
MvC2 + |
1
2
|
Jpw2, |
| (44) |
Thus, in plane motion, the kinetic energy of a body is equal to the kinetic
energy of translation of the centre of mass plus the kinetic energy of
rotation relative to the centre of mass.
(4)* The Most General Motion of a Body . Taking the centre of mass Ñ
as the pole (Fig. 317), the most general motion of a body is a combination of a
translation with the velocity vc of the pole and
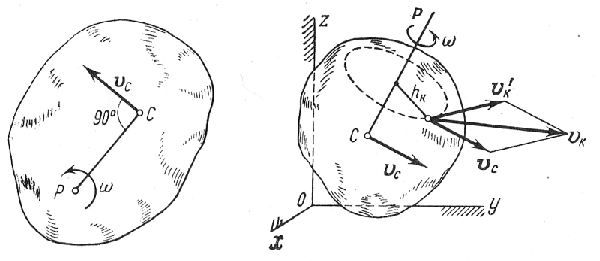Fig. 316 Fig. 317
a rotation about the instantaneous axis CP through the pole (see § 88). Then,
as shown in the course of kinematics, the velocity vk of any point of
the body is equal to the geometrical sum of the velocity vc of the pole
and the velocity v¢k of the point in its rotation with the body about axis
CP:
In magnitude v¢k = whk, where hk is the distance of the point from
axis CP and ñî is the absolute angular velocity of the body about that axis.
It follows from this that2
|
vk2 = |
®
v
|
2
k
|
= ( |
®
v
|
c
|
+ |
®
v¢
|
k
|
)2 = vc2 + v¢k2 + 2 |
®
v
|
c
|
· |
®
v¢
|
k
|
. |
|
Substituting this expression into Eq. (41) and taking into account that
v¢k = whk, we find:
|
T = |
1
2
|
|
æ
è
|
å
| mk |
ö
ø
|
vC2+ |
1
2
|
|
æ
è
|
å
| mkhk2 |
ö
ø
|
w2+ |
®
v
|
c
|
· |
å
| mk |
®
v¢
|
k
|
, |
|
where the common multipliers have been taken outside of the parentheses.
In this equation, the term in the first parentheses gives the mass M of the
body and the term in the second parentheses gives the moment of inertia
JCP of the body with respect to the instantaneous axis CP. In the last term
åmkv¢k = 0 as it represents the linear momentum of the body in its rotation
about axis CP, which passes through the centre of mass (see § 138).
Therefore, we finally have:
|
T = |
1
2
|
Mvc2 + |
1
2
|
JCPw2. |
| (45) |
Thus, in the most general motion of a body, the kinetic energy is equal to
the kinetic energy of translation of the centre of mass of the body plus the
kinetic energy of rotation about an axis through the centre of mass.
If the pole is taken not in the centre of mass but in another point A such
that axis AA¢ does not pass through the centre of mass, then for this axis
åmkv¢k ¹ 0, and we cannot develop an equation of the form (45) (see
Problem 136).
Footnotes:
1This case can be developed as a particular case of the most general
motion of a rigid body discussed in the following item.
2From the definition of the scalar product of two vectors (see footnote on
p. 300) it follows that v2 = v·v = vvcos0 = v2, i.e., the scalar
square of a vector is equal to the square of its magnitude. This result has
been employed here.
|
File translated from
TEX
by
TTH,
version 3.64.
On 24 Apr 2005, 09:36.
|