МЕТОД УПРУГОГО ЭКВИВАЛЕНТА ДЛЯ МОНИТОРИНГА БИФУРКАЦИЙ ВЫСОКИХ ПОРЯДКОВ СОСУДОВ

ПРИ ВЫСОКОМ ДАВЛЕНИИ

М.Н.Кирсанов

(Москва, Московский энергетический институт (ТУ), Россия)

       Для безопасной эксплуатации теплоэнергетических установок, работающих под большим давлением и высокой температуре, требуется не только качественная оценка напряженно-деформированного состояния конструкций в процессе ее работы, но и контроль возможной потери устойчивости. Особенность работы современных энергетических установок (в том числе и термоядерных)  состоит  в том, что они подвержены нестационарным воздействиям, приводящим в критических условиях к потери устойчивости. Целью данной работы является учет характера нестационарных воздействий для расчета устойчивости конструкции из материала, обладающего свойством ползучести при высоких температурах (сталь, сплавы). Старение материала и изменение расчетной схемы (геометрия, нагрузка и граничные условия) не учитываются.

      Существуют различные теории, описывающие явление потери устойчивости ползущих систем. Обзор подходов содержится в [1,2,3]. Нестационарные воздействия, например, градиенты температуры, изменение давления и другие возмущения параметров работы установки, приводят к изменениям деформации конструкции, наблюдаемым в виде изменений ее прогиба.  Рассмотрим какую-нибудь характерную точку конструкции, в которой изменение прогиба со временем, вызванное возмущениями различной природы, опишем как скалярную функции времени . Будем предполагать, что эта функция является непрерывной. Нестационарность воздействий приводит к изломам кривой . Те точки, кривой, где терпит разрыв N-я производная  будем называть точками возмущения N-го порядка. Величина разрыва для анализа устойчивости не существенна. Теоретически будем предполагать, что разрыв как угодно мал. Основы теории устойчивости по отношению к возмущениям высших производных по времени прогиба конструкции заложены  в [4,5]. Развитие теории применительно к пространственным системам  на основе метода упругого эквивалента дано в [6,7]. Метод упругого эквивалента  является  эффективным приемом решения задач со  сложной реологией. Метод основан на сведении исходной постановки  к  решению задачи  устойчивости  некоторой  упругой  конструкции  с  модулем упругости (или матрицей упругости), зависящим от времени.

  Рассмотрим  определяющее  соотношение  теории течения

где - компоненты скорости деформации ползучести, G – модуль сдвига,  девиатор напряжений,   - параметры    материала, , . Cвязь приращений девиатора напряжений и деформации  для  упругого эквивалента среды имеет форму закона Гука , N=0,1,2..

Верхний  индекс  в  скобках  указывает  на  порядок   возмущаемой

производной. Получена следующая матрица [6]

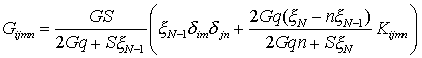                     (1)

- тензор, определяемый напряженным состоянием конструкции,  - известные функции [4], , .. . Матрица определяет связь приращений напряжений и деформацией в особой точке порядка N. В особой точке возмущение производной прогиба порядка N приводит к неограниченному росту прогиба, приводящему к выпучиванию [4]. Аналогичная   матрица    для    соотношения    ползучести деформационного типа , , ,  имеет вид  [7]

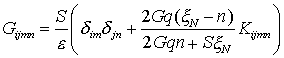                                                            (2)

Сравнение матриц  (1) и  (2)  показывает,  что  в  первом  случае (теория  течения) матрица,  отвечающая  возмущению    производной порядка N, содержит значения  и  - корни полиномов порядка  N  и  N-1,  которые  могут  и  не существовать одновременно, в то время как (2) содержит лишь . Функции   табулированы [4]. Замечено, что для малых  значений  c четными индексами не  существует. Следовательно, теория ползучести типа течения не выделяет критических ситуаций по отношению к возмущениям производных прогиба определенных (как правило низких) порядков там, где деформационная теория дает реальные результаты. Таким образом, проблема выбора критического номера особой точки для рассмотренных теорий решается по-разному. Первой в процессе деформирования критической ситуацией по теории течения может быть особая точка сравнительно высокого порядка, в то время как по деформационной теории на этот же момент будет указывать точка сгущения особых точек, безопасно пройденных системой вплоть до критического момента. Заметим,  что  матрицы  (1,2) найдены   без  привлечения  уравнений равновесия  и  каких-либо  краевых  условий  конкретных задач. Окончательное решение – зависимость критической  нагрузки и критического времени (гарантийного срока) получится  на  основе матрицы упругого эквивалента при подстановке ее в готовое решение задачи  устойчивости  упругой  системы  – упругого  эквивалента исследуемой конструкции. Простота матриц позволяет  во многих случаях  вывести аналитическое  решение.  Когда  решение задачи  устойчивости  для   упругой    системы    невозможно    в аналитической форме, допустимо приближенное численное  решение  с использованием полученных  матриц.  Алгоритм  решения  состоит  в поиске корней определителя, к  которому  обычно  сводится  задача упругой устойчивости, где время является искомой  величиной. Время (или  деформация  ползучести,  монотонно  с  ним  связанная кривой ползучести докритического деформирования) входит в решение через коэффициенты матрицы упругого эквивалента.

      Приведем пример простого аналитического решения, полученного с использованием матрицы (2). Рассмотрим явление потери устойчивости (сплющивание) цилиндрической оболочки длиной l, радиуса R под равномерным боковым давлением Q. Толщина оболочки h. Материал оболочки удовлетворяет приведенным выше соотношениям деформационной теории ползучести. Введены два существенных упрощающих предположения. Во-первых, пренебрегаются упругие деформации по сравнению с деформациями ползучести. Такая гипотеза традиционна для подобных задач. Во-вторых, принимается определяющее соотношение ползучести  без упрочнения: . Формальное решение задачи об особых точках при  не дает решения, т.к. четных   не существует, а . Однако замечено, что решение задачи в зависимости от   имеет при   скачок. Это следует из того, что функции  обнаруживают в нуле бесконечную производную. Поэтому, предполагая, что коэффициент упрочнения   не ноль, а какая-то малая неулавливаемая из экспериментальных кривых ползучести величина,  заменим нулевые значения   их значениями на скачке [9]. Стандартные уравнения равновесия технической теории оболочек и известная методика определения критической нагрузки, включающая минимизацию по параметрам волнообразования, дают простую формулу для критической нагрузки. Замена упругих констант, входящих в эту формулу, на элементы матрицы (2), зависящие от времени, дает после некоторых преобразований следующее решение для критического времени

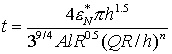                                                                                       (3)

где  -   функция, определяемая аппроксимацией кривой решения в зависимости от    в нуле. При n=1 имеем , , , , . Четные особые точки для малых  и, следовательно, в "условном" нуле не существуют. С увеличением степени n значение   падает и для n>6 эта функция имеет приблизительно постоянное значение: , , , , .

ЛИТЕРАТУРА

1.     Drozdov    A.D.,Kolmanovskii V.B. Stability in Viscoelasticity.- Netherlands: Elsiver Science,1994.- 600 p.

2.     Потапов  В.Д. Устойчивость вязкоупругих элементов конструкций.-- М.: Стройиздат, 1985. - 312 с.

3.     Куршин Л.М. Устойчивость при ползучести// Изв.АН СССР. МТТ. – 1978.-  N3. - С.  125-160.

4.     Кирсанов М.Н., Клюшников В.Д. Определение особых точек процесса деформирования сжатого стержня в условиях ползучести//Изв.АН  СССР.  МТТ.  -  1993.-N3.- С.143-150.

5.     Клюшников  В.Д.  Лекции  по  устойчивости    деформируемых систем.- М.: МГУ, 1986.- 224 с.

6.     Кирсанов  М.Н.  Выпучивание    слоистой    пластины    при ползучести// Проблемы  машиностроения  и  надежности    машин.- 1994.- N4.- С. 53-58.

7.     Кирсанов  М.Н., Клюшников  В.Д.  Особые   точки    процесса деформирования и выпучивание цилиндрической оболочки в условиях ползучести// ПМТФ.- 1994.-N5.- С.128-135.

8.     Кирсанов М.Н. Учет погрешности аппроксимации в решении задачи выпучивания при установившейся ползучести по теории особых точек// Современные проблемы механики и математической физики. Воронеж: ВГУ, 1994. - С.49.

Рассматриваются теоретические вопросы и решения  некоторых  задач

выпучивания  строительных  конструкций  с    учетом    нелинейной

ползучести материала.

Reological problems of structures

Kirsanov M.N