1.1. Понятие множества
При изложении теории множеств мы будем придерживаться так называемой
интуитивной точки зрения, согласно которой такие понятия, как
"множество", "элемент множества", относятся к начальным
(примитивным) понятиям математики и поэтому не подлежат определению.
Математическое понятие множества постепенно выделилось из привычных
представлений о совокупности, собрании, классе и т.д. Один из создателей
теории множеств - Георг Кантор1
представлял множество как "совокупность или набор определенных и различимых
между собой объектов, мыслимых как единое целое".
С понятием множества мы соприкасаемся прежде всего тогда, когда по
какой-либо причине объединяем по некоторому признаку в одну группу какие-то
объекты и далее рассматриваем эту группу или совокупность как единое целое.
Множества принято обозначать заглавными латинскими буквами. Объекты, которые
образуют множество, называют элементами множества и для обозначения элементов
используют, как правило, малые буквы латинского алфавита. Если a является
элементом множества M, то будем говорить, что a принадлежит множеству M, и
использовать запись a О M, в противном случае, если a не принадлежит множеству M,
будем использовать обозначение a П M.
В различных приложениях дискретной математики чаще всего встречаются
конечные множества. Интуитивный смысл этого термина ясен: такие множества содержат конечное
число элементов. Число элементов конечного множества A называют
мощностью этого множества и обозначают символом Card A
или |A|. Наряду с конечными множествами в математике
рассматривают и бесконечные множества, то есть такие, которые
содержат бесконечно много элементов. Так, например, бесконечно множество
натуральных чисел N, множество рациональных чисел Q,
множество действительных чисел R.
Способы задания множеств
Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы
множества записывают внутри фигурных скобок, например: А = { 1, 2, a, x } или B = { река Нил, город Москва, планета
Уран}.
Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись A = { x|P( x ) }, которую читают следующим
образом: "A есть множество элементов x таких, что для них выполняется
свойство P( x )".
Например, B = { x| x- натуральное число, меньшее 10 }, при
этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.
Множество можно задать порождающей процедурой, например:
D = { z|1 О D,и если z О D,то z + 3 О D},
E = { x| x = 3k, k - любое нартуральное число.}
Наряду с порождающей процедурой существует распознающая или разрешающая процедура, которая
позволяет определить, принадлежит ли данный объект множеству или нет. Для
множества D распознающая процедура заключается в том, что для любого
натурального числа n будут проверять, является ли число 3 делителем числа
n - 1. Для множества E распознающая процедура заключается в разложении
числа на простые множители.
Пустое и универсальное множества
Определение 1.1. В теории множеств отдельно вводится множество,
которое не содержит ни одного элемента. Такое
множество называется пустым и обозначается символом
Ж.
В любой конкретной задаче приходится иметь дело только с подмножествами
некоторого, фиксированного для данной задачи, множества. Его принято
называть универсальным и обозначать символом U.
Например, при сборке некоторого изделия универсальным множеством естественно
назвать множество всех деталей и сборочных элементов, из которых это изделие
состоит.
Если мы рассматриваем множества, связанные с какими-нибудь фигурами на
плоскости, то в качестве универсального множества можно выбрать множество
всех точек плоскости.
Определение 1.2. Два множества A и B называются равными (A = B), если
они состоят из одних и тех же элементов. Поэтому несуществен порядок записи
в фигурных скобках элементов множества, задаваемого списком, т.е.
{ a, b, c } = { a, c, b }.
Операции над множествами
Определение 1.3. Множество A называется
подмножеством множества B, если любой элемент множества A
принадлежит множеству B. При этом пишут A М B, где " М "
есть знак вложения подмножества. Из определения следует, что для любого
множества A справедливы, как минимум, два вложения A М A и A М U.
Определение 1.4. Если A М B и A № B, A № Ж,
то A называетсясобственным подмножеством множества B. В этом
случае B содержит хотя бы один элемент, не принадлежащий A.
В теории множеств, по определению, полагают, что пустое множество является
подмножеством любого множества: Ж М A.
Пустое множество и само множество A называются несобственными подмножествами множества A.
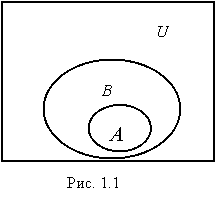
При графическом изображении множеств удобно использовать диаграммы
Венна , на которых универсальное множество обычно
представляют в виде прямоугольника, а остальные множества в виде овалов,
заключенных внутри этого прямоугольника (рис 1.1).
 Определение 1.5.Объединением множеств A и B
(обозначение A ИB) называется множество элементов x таких, что x
принадлежит хотя бы одному из двух множеств A или B (рис 1.2).
Символически это можно записать следующим образом:
A ИB = {x|x О A или x О B}.
Определение 1.5.Объединением множеств A и B
(обозначение A ИB) называется множество элементов x таких, что x
принадлежит хотя бы одному из двух множеств A или B (рис 1.2).
Символически это можно записать следующим образом:
A ИB = {x|x О A или x О B}.
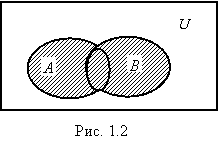 Определение 1.6. Пересечением множеств A и B
(обозначение A ЗB) называется множество, состоящее из элементов x,
которые принадлежат и множеству A и множеству B (рис. 1.3):
A ЗB = {x|x О A и x О B}.
Определение 1.6. Пересечением множеств A и B
(обозначение A ЗB) называется множество, состоящее из элементов x,
которые принадлежат и множеству A и множеству B (рис. 1.3):
A ЗB = {x|x О A и x О B}.
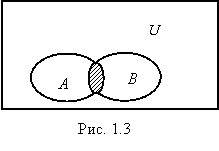 Определение 1.7. Разностью множеств A и B
называется множество всех тех элементов множества A, которые не
принадлежат множеству B (рис. 1.4):
A\B = {x|x О A и x П B}.
Определение 1.7. Разностью множеств A и B
называется множество всех тех элементов множества A, которые не
принадлежат множеству B (рис. 1.4):
A\B = {x|x О A и x П B}.
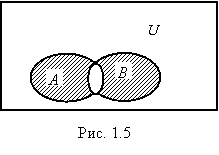
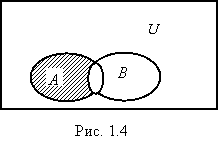 Определение 1.8. Симметрической разностью множеств A и B
называется множество AD B = ( A\B )И( B\A ) (рис. 1.5).
Определение 1.8. Симметрической разностью множеств A и B
называется множество AD B = ( A\B )И( B\A ) (рис. 1.5).
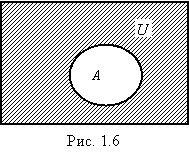
 Определение 1.9.
Абсолютным дополнением множества A называется
множество всех элементов, не принадлежащих A, т.е. множество `A = U\A, где U - универсальное множество (рис. 1.6).
Определение 1.9.
Абсолютным дополнением множества A называется
множество всех элементов, не принадлежащих A, т.е. множество `A = U\A, где U - универсальное множество (рис. 1.6).
 В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять
термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять
термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
|
A ИB = { a , c, d, e, f, h }, A ЗB = { c, e }, A\B = {d}, |
|
|
A D B = { a, d, f, h }, |
A
|
= { a, b, f, g, h }. |
|
Свойства операций
Для любых множеств A,B,C выполняются следующие тождества:
- A ИB = B ИA, A ЗB = B ЗA
(коммутативность объединения и пересечения);
-
A И( B ИC ) = ( A ИB ) ИC, A З( B ЗC ) = ( A ЗB ) ЗC
(ассоциативность объединения и пересечения);
-
A З( B ИC ) = ( A ЗB ) И( AЗC ),
A И( B ЗC ) = ( A ИB ) З( AИC )
(дистрибутивность;
-
A ИA = A, A ЗA = A
(идемпотентность;
-
A ИU = U, A ЗU = A, A ИЖ = A, A ЗЖ = Ж,
-
A И`A = U, A З`A = Ж
(свойства универсального и пустого множеств);
-
(закон двойного дополнения;
-
|
|
A ИB
|
= |
-
A
|
З |
-
B
|
, |
A ЗB
|
= |
-
A
|
И |
-
B
|
|
|
(законы де Моргана).
Посмотрим, как доказываются свойства операций над множествами. Прежде всего
отметим, что, согласно определению, для доказательства равенства двух
множеств E = F необходимо установить справедливость двух вложений E М F и F М E.
Теперь приведем доказательства, например, третьего и седьмого свойств.
Доказательство равенства: A З( B ИC ) = ( A ЗB ) И( A ЗC ).
· Покажем сначала, что A З( B ИC ) М
( A ЗB ) И( A ЗC ). Пусть x О AЗ( B ИC ). Это означает, что x О A и x О B ИC, поэтому x О A и x принадлежит хотя бы одному из двух множеств B
или C.
Если мы предположим, что x О В, то x О A ЗB и,
следовательно2, x О ( A ЗB ) И( AЗC ). Если же предположить, что x О C, то x О A ЗC и
поэтому x О ( A ЗB ) И( A ЗC ).
Таким образом, вложение A З( B ИC ) М ( AЗB ) И( A ЗC ) доказано.
Докажем справедливость обратного вложения:
|
A З( B ИC ) Й ( A ЗB ) И( A ЗC ). |
|
Пусть x О ( A ЗB ) И( A ЗC ), это
означает, что x принадлежит хотя бы одному из двух множеств A ЗB или
A ЗC. Если x О A ЗB, то x О A и x О B. Следовательно,
x О A и x О B ИC, т.е. x О A З( B ИC ).
Если же x О A ЗC, то x О A и x О C, и тогда x О A и x О C ИB, т.е. x О A З( C ИB ) = A З(B ИC ). ·
Наряду с объединением и пересечением двух множеств можно рассматривать
объединение и пересечение любого конечного (или бесконечного) числа
множеств. При этом обычно используют следующие формы записи:
|
B = |
k
И
i = 1
|
Ai , С = |
Ґ
И
i = 1
|
Ai . |
|
Пример 1.2. X = { 1,2,3 }, Y = { 1,2}, Z = { 1,2,3,{ 1,2 } }.
Определить, какие из приведенных ниже утверждений справедливы, а какие -
нет:
а) 1 О X, b) 1 М X, c) Y О X, d) Y М X, e) Y О Z, f) Y М Z.
Утверждение а) справедливо, так как 1 является элементом множества X;
b) неверно, так как 1 не является подмножеством множества X;
c) несправедливо, так как множество Y не является элементом множества X,
и поэтому Y не принадлежит множеству X;
d) справедливо, так как множество Y является подмножеством множества X;
e) справедливо, так как множество Y является элементом множества Z;
f) справедливо, так как множество Y является подмножеством множества Z.
Пример 1.3. Определить, какие из приведенных утверждений справедливы,
а какие нет:
|
a) Ж О Ж, b) Ж М Ж, c) Ж О { Ж}, d) Ж М { Ж}. |
|
Утверждение а) неверно, так как пустое множество по определению не содержит
элементов;
b) справедливо, так как пустое множество есть подмножество любого множества,
в том числе и пустого;
c) справедливо, так как представленное множество { Ж} содержит один элемент - Ж;
d) справедливо, так как пустое множество является подмножеством любого
множества, в том числе и множества { Ж}.
Пример 1.4. Рассмотрим множество всех натуральных чисел N и три
множества A = { 1,2 }, B = N\A, C = {A,B }. Справедливо ли высказывание 1 О C?
На первый взгляд кажется, что множество C содержит любое натуральное
число, однако на самом деле множество С вообще не содержит ни одного
натурального числа. Действительно, 1 № A, 1 № B, и поэтому 1 П C.
Парадокс Рассела
Парадокс Рассела демонстрирует несовершенство и
недостаточность интуитивных представлений о множествах3. Прежде чем привести формулировку
парадокса Рассела, остановимся на трех важных моментах.
Существуют множества, которые содержат другие множества в качестве своих
элементов; таким является, например, множество Z из примера 1.2.
Существуют множества, которые не являются элементами самих себя, например,
множество A = { 1,2 } не является числом и A П A.
Если какое-то множество определено корректно, то всегда (имеется в виду -
для любого объекта) должен существовать однозначный ответ на вопрос, принадлежит ли
выбранный объект данному множеству.
Теперь рассмотрим множество F, содержащее те и только те множества,
которые не являются элементами самих себя:
F = { M| M- множество и M П M }.
Парадокс состоит в том, что после такого способа задания множества F мы не
можем однозначно ответить на вопрос: само множество F как элемент принадлежит F или
нет?
В самом деле, если мы предположим, что F О F, то тогда F является
элементом самого себя и не может, согласно определению, принадлежать F,
т.е. F П F.
Если же предположить, что F П F, то это означает, что F не является
элементом самого себя и поэтому F как элемент принадлежит F, т.е. F О F.
"Житейским" или ситуационным аналогом парадокса Рассела является известный
рассказ о брадобрее.
Брадобрей воинской части получает приказ от командира брить всех тех, кто не
бреется сам, но при этом, в целях экономии времени, ему запрещено брить всех
тех, кто бреется самостоятельно. Теперь зададим вопрос: может ли брадобрей
побрить самого себя?
Если ответ - "да", то он принадлежит к тем, кто бреется самостоятельно,
но таких ему брить запрещено. Если - "нет", то он принадлежит к тем, кто
сам не бреется, а такого человека он брить обязан.
Булеан множества
Напомним, что число элементов конечного множества называется мощностью множества и обозначается символом |A| или Card A
(от английского cardinality - мощность).
Определение 1.10. Множество всех подмножеств данного множества
называют булеаном множества. Булеан обозначают символом
B(A).
Пример 1.5. Пусть A = { 1,2,3 }. Перечислить элементы
булеана множества A.
B(A)={ Ж,{ 1 },{ 2 },{ 3},{ 1,2 },{ 1,3 },{ 2,3},{ 1,2,3 } }.
Пример 1.6. Пусть A = { 1,2,3,4,...,n }, т.е. |A | = n. Найдем мощность множества B(A).
Для определения CardB(A) воспользуемся биномиальными коэффициентами
Cnk (число сочетаний из n по k)4.
Перечислим по порядку, начиная с пустого множества, все подмножества
множества A:
- пустому подмножеству Жмножества A поставим в соответствие число
1 = Cn0;
-
булеан содержит одноэлементные подмножества:
|
{ 1 }, { 2 }, { 3 }, ..., {n}. |
|
Число одноэлементных подмножеств равно n = Cn1;
-
булеан содержит следующие двухэлементные подмножества:
|
{ 1,2 },{ 1,3 },{ 1,4 }, ј,{ 1,n },{ 2,3 },{ 2,4 }, ј,{ 2,n }, |
|
|
{ 3,4 },{ 3,5 }, ј,{ 3,n }, ј,{ n - 2,n - 1 },{ n - 2,n },{ n - 1,n}. |
|
Количество двухэлементных подмножеств равно
-
продолжая этот подсчет, получим, что булеан содержит Cn3
трехэлементных подмножеств, Cn4 четырехэлементных
подмножеств и так далее;
-
наконец, мы отметим, что булеан содержит Cnn - 1
(n - 1)-элементных подмножеств и одно n-элементное подмножество - само
множество A, которому мы сопоставим биномиальный коэффициент Cnn = 1.
В результате сумма всех биномиальных коэффициентов покажет нам количество
элементов булеана B(A):
|
2n = (1 + 1)n = Cn0 + Cn1 + Cn2 + ... + Cnn - 1 +Cnn . |
|
Таким образом, для любого множества A, если Card A = n, то Card
B(A)=2n.
Footnotes:
1 Кантор Георг (1845-1918) -
немецкий математик, основатель теории множеств.
2 Если x О A ЗB, то x О ( A ЗB) ИD, где символом D обозначено любое множество. В данном
случае D = A ЗC.
3 Рассел
Бертран Артур Вильям (1872-1970) - английский логик, философ, математик,
социолог и общественный деятель.
4
показывает,
сколько существует способов для выбора из n различных элементов k
различных элементов, если порядок их следования не имеет значения.
|
 Определение 1.5.Объединением множеств A и B
(обозначение A ИB) называется множество элементов x таких, что x
принадлежит хотя бы одному из двух множеств A или B (рис 1.2).
Символически это можно записать следующим образом:
A ИB = {x|x О A или x О B}.
Определение 1.5.Объединением множеств A и B
(обозначение A ИB) называется множество элементов x таких, что x
принадлежит хотя бы одному из двух множеств A или B (рис 1.2).
Символически это можно записать следующим образом:
A ИB = {x|x О A или x О B}.
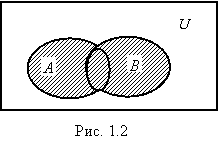 Определение 1.6. Пересечением множеств A и B
(обозначение A ЗB) называется множество, состоящее из элементов x,
которые принадлежат и множеству A и множеству B (рис. 1.3):
A ЗB = {x|x О A и x О B}.
Определение 1.6. Пересечением множеств A и B
(обозначение A ЗB) называется множество, состоящее из элементов x,
которые принадлежат и множеству A и множеству B (рис. 1.3):
A ЗB = {x|x О A и x О B}.
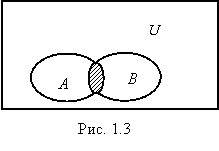 Определение 1.7. Разностью множеств A и B
называется множество всех тех элементов множества A, которые не
принадлежат множеству B (рис. 1.4):
A\B = {x|x О A и x П B}.
Определение 1.7. Разностью множеств A и B
называется множество всех тех элементов множества A, которые не
принадлежат множеству B (рис. 1.4):
A\B = {x|x О A и x П B}.
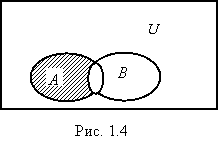 Определение 1.8. Симметрической разностью множеств A и B
называется множество AD B = ( A\B )И( B\A ) (рис. 1.5).
Определение 1.8. Симметрической разностью множеств A и B
называется множество AD B = ( A\B )И( B\A ) (рис. 1.5).
 Определение 1.9.
Абсолютным дополнением множества A называется
множество всех элементов, не принадлежащих A, т.е. множество `A = U\A, где U - универсальное множество (рис. 1.6).
Определение 1.9.
Абсолютным дополнением множества A называется
множество всех элементов, не принадлежащих A, т.е. множество `A = U\A, где U - универсальное множество (рис. 1.6).
 В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять
термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять
термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то