15  Экстремумы функции двух переменных

1. Теорема. Необходимые условия экстремума
   Если функция z=f(x,y) достигает экстремума при. x=x₀, y=y₀, то каждая частная производная первого порядка от z или обращается в нуль или не существует (x=x₀, y=y₀ - критическая точка).
   Теорема не является достаточной для определения максимума или минимума.
   Пример.
   

   z=x2-y2

   
   

   ¶z ¶x =2x, ¶z ¶y = - 2y

   
   
   
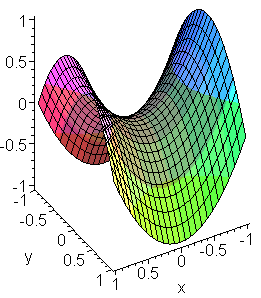
   Очевидно, производные равны 0 при x=0, y=0, но экстремума нет. Такая особенность функции называется седлом.
2. Введем обозначения для производных
   

   ¶2f ¶x2 =A, ¶2f ¶xy =B, ¶2f ¶y2 =C.

   Теорема. Пусть в некоторой области, содержащей точку M₀(x₀,y₀), функция f(x,y) имеет непрерывные частные производные до третьего порядка включительно. Если точка M₀(x₀,y₀) является критической
   

   ¶f ¶x =0, ¶f ¶y =0

   то при x=x₀, y=y₀
   1. f(x,y) имеет максимум, если AC-B² > 0, A < 0;
   2. f(x,y) имеет минимум, если AC-B² > 0, A > 0;
   3. f(x,y) не имеет ни максимума, ни минимума, если AC-B² < 0;
   4. требуется дополнительное исследование, если AC-B²=0.
   Доказательство. По формуле Тейлора
   

   f(x0+Dx,y0+Dy) = f(x0,y0)+ ¶f(x0,y0) ¶x Dx+ ¶f(x0,y0) ¶y Dy+

   
   

   + 1 2 (ADx2+2BDxDy+CDy2)+a(Dr)3

   где
   

   Dr = Ц   Dx2+Dy2   ,

   а a стремится к 0 при Dr® 0. Так как в критической точке ¶f/¶x=0, ¶f/¶y=0, то
   

   Df= 1 2 (ADx2+2BDxDy+CDy2)+a(Dr)3

   (1)

   Обозначим Dx=Drcosj, Dy=Drsinj. Преобразуем (1)
   

   Df= 1 2 Dr2(Acos2j+2Bcosjsinj+Csin2j)+a(Dr)3

   (1)

   
   

   Df= 1 2 Dr2 ж и (Acosj+Bsinj)2+(AC-B2)sin2j A ц ш +a(Dr)3

   (2)

   Доказательство теоремы следует из анализа (2).
   1. Пусть AC-B² > 0. Тогда (Acosj+Bsinj)²+(AC-B²)sin²j > 0. При A < 0 имеем Df < 0 (максимум), а при A > 0 имеем Df > 0 (минимум).
   2. Пусть AC-B² < 0, A > 0. Тогда при sin²j = 0 из (2) следует
      

      Df= 1 2 Dr2(A+a(Dr)3) > 0,

      т.е. функция возрастает от критической точки на этом направлении. При Acosj+Bsinj = 0 из (2) следует
      

      Df= 1 2 Dr2 ж и (AC-B2)sin2j) A ц ш +a(Dr)3 < 0,

      т.е. функция уменьшается от критической точки на этом направлении. Таким образом в критической точке нет ни максимума ни минимума. Аналогично исследуется случай A < 0 и случай AC-B² < 0, A=0.