Элементы математической логики
Определение 4. Импликацией высказываний ![]() ,
,
![]() называется
высказывание
называется
высказывание ![]() («если
(«если
![]() , то
, то ![]() », «из
», «из ![]() следует
следует ![]() »), которое ложно в том
и только в том случае, когда
»), которое ложно в том
и только в том случае, когда ![]() истинно, а
истинно, а ![]() ложно (табл. 4). Высказывание
ложно (табл. 4). Высказывание ![]() называют посылкой, а высказывание
называют посылкой, а высказывание ![]() –
заключением импликации.
–
заключением импликации.
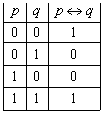
Определение 5. Эквиваленцией высказываний ![]() ,
,
![]() называется
высказывание
называется
высказывание ![]() («
(«![]() равносильно
равносильно ![]() »), которое истинно
тогда и только тогда, когда значения истинности высказываний
»), которое истинно
тогда и только тогда, когда значения истинности высказываний ![]() и
и ![]() совпадают (табл. 5).
совпадают (табл. 5).
Табл. 5
Теперь обсудим подробнее смысл и практику применения различных логических связок.
Обычно введение с помощью перечисленных таблиц
истинности операций отрицания, конъюнкции и дизъюнкции не вызывает
необходимости каких-то специальных пояснений или оговорок. Так, например,
дизъюнкцию двух высказываний «сегодня идет снег» (высказывание ![]() ) или «сегодня идет
дождь» (высказывание
) или «сегодня идет
дождь» (высказывание ![]() )
можно признать истинной и в том случае, когда на улице идет только снег
(третья строка табл. 3), и тогда, когда на улице идет только дождь (вторая
строка таблицы), и в том случае, когда на улице идет снег с дождем (последняя
строка таблицы). Если же сегодня на улице нет дождя и нет снегопада, то
указанную дизъюнкцию следует признать ложной (первая строка табл.3).
)
можно признать истинной и в том случае, когда на улице идет только снег
(третья строка табл. 3), и тогда, когда на улице идет только дождь (вторая
строка таблицы), и в том случае, когда на улице идет снег с дождем (последняя
строка таблицы). Если же сегодня на улице нет дождя и нет снегопада, то
указанную дизъюнкцию следует признать ложной (первая строка табл.3).
При обсуждении импликации сначала рассмотрим следующий пример.
Пример 1. Пусть множество ![]() есть подмножество некоторого
множества
есть подмножество некоторого
множества ![]() (
(![]() ). Рассмотрим два
высказывания
). Рассмотрим два
высказывания ![]() и
и
![]() соответственно:
«элемент
соответственно:
«элемент ![]() » и
«элемент
» и
«элемент ![]() ».
Тогда импликации
».
Тогда импликации ![]() соответствует
следующее высказывание: «если элемент
соответствует
следующее высказывание: «если элемент ![]() , то элемент
, то элемент ![]() ».
».
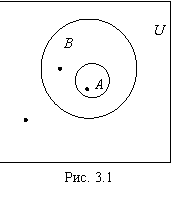 При этом трем различным положениям
точки, отвечающей элементу
При этом трем различным положениям
точки, отвечающей элементу ![]() на рис. 1, можно сопоставить три строки
таблицы 4, в каждой из которых импликация принимает значение «истина».
Действительно, ситуация, когда
на рис. 1, можно сопоставить три строки
таблицы 4, в каждой из которых импликация принимает значение «истина».
Действительно, ситуация, когда ![]() и
и ![]() , возможна, этой ситуации соответствует
строка
, возможна, этой ситуации соответствует
строка ![]() таблицы
4. Точно так же возможны еще два расположения точки
таблицы
4. Точно так же возможны еще два расположения точки ![]() – когда
– когда ![]() и
и ![]() (строка
(строка ![]() ) и когда
) и когда ![]() и
и ![]() (строка
(строка ![]() ). Наконец, в рамках нашего условия (
). Наконец, в рамках нашего условия (![]() ) абсолютно невозможно
представить ситуацию, когда элемент
) абсолютно невозможно
представить ситуацию, когда элемент ![]() и одновременно элемент
и одновременно элемент ![]() (строка
(строка ![]() ). Таким образом, именно в том
случае, когда посылка истинна, а заключение ложно, импликацию
). Таким образом, именно в том
случае, когда посылка истинна, а заключение ложно, импликацию ![]() следует признать
ложной.
следует признать
ложной.
Еще одно известное обоснование введения
импликации с помощью таблицы 4 заключается в том, что импликация вводится
таким образом, чтобы два составных высказывания: «из ![]() и
и ![]() следует
следует ![]() » и «из
» и «из ![]() и
и ![]() следует
следует ![]() » всегда, т.е. при любых значениях истинности
высказываний
» всегда, т.е. при любых значениях истинности
высказываний ![]() ,
,
![]() , принимали
только значение «истина».
, принимали
только значение «истина».
Пример 2. Рассмотрим еще одну импликацию: «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной.
Вместе с тем необходимо отметить, что во
множестве других случаев попытка отождествить импликацию с традиционным понятием
логического следования может приводить к самым удивительным результатам. Так,
например, в соответствии с таблицей 4 следует признать истинной следующую
импликацию: «если ![]() ,
то Москва является столицей России». С точки зрения обыденной логики такая
ситуация целиком абсурдна, но это мнение возникает в силу того, что
человеческий разум пытается, в первую очередь, придать импликации смысл
причинной логической связи, т.е. подразумевается, что заключение может быть
выведено из посылки на основании каких-то логических рассуждений. Однако
абсолютная чужеродность посылки и заключения оставляет лишь одну возможность –
руководствоваться формальным определением импликации.
,
то Москва является столицей России». С точки зрения обыденной логики такая
ситуация целиком абсурдна, но это мнение возникает в силу того, что
человеческий разум пытается, в первую очередь, придать импликации смысл
причинной логической связи, т.е. подразумевается, что заключение может быть
выведено из посылки на основании каких-то логических рассуждений. Однако
абсолютная чужеродность посылки и заключения оставляет лишь одну возможность –
руководствоваться формальным определением импликации.
Замечание. Можно сказать, что формальное определение импликации гораздо ближе искусственному интеллекту, чем традиционному мышлению человека, поскольку импликация может быть реализована в операторах условного перехода в программировании, а также в некоторых компьютерных микросхемах. Тем удивительнее тот факт, что еще в глубокой древности Аристотель уже знал, что импликация истинна в трех из четырех случаев, а философы стоической школы (IV-III вв. до н.э.) подразумевали современную таблицу истинности для импликации. Стоики древней Греции были убеждены, что Земля абсолютно неподвижна, и приведенные ниже дословные суждения стоиков следует рассматривать именно с этой точки зрения[2]:
1. Если день, то свет (истинно).
2. Если Земля летает, то она имеет крылья (истинно).
Если Земля существует, то она летает (ложно).
4. Если Земля летает, то она существует (истинно).
Формулы логики высказываний. Общезначимые,
выполнимые и противоречивые формулы
Переменные, обозначающие
высказывания, логические связки ┐, ![]() ,
,
![]() ,
,![]() ,
, ![]() , символы скобок ) и ( составляют
алфавит логики высказываний. С помощью этого алфавита мы можем конструировать
различные логические формулы.
, символы скобок ) и ( составляют
алфавит логики высказываний. С помощью этого алфавита мы можем конструировать
различные логические формулы.
Определение 6. Выражение называется логической формулой (пропозициональной формулой), если это выражение удовлетворяет следующим условиям:
1) любая логическая переменная есть формула;
2) если
![]() и
и ![]() — формулы, то (┐
— формулы, то (┐![]() ), (
), (![]()
![]()
![]() ), (
), (![]()
![]()
![]() ), (
), (![]()
![]()
![]() ), (
), (![]()
![]()
![]() ) тоже являются
формулами;
) тоже являются
формулами;
3) других формул нет.
Пример 3. Выражение ![]() ┐
┐![]() не является формулой, а запись
не является формулой, а запись ![]() ┐
┐![]() )) представляет собой формулу.
Действительно, в первом выражении между высказыванием
)) представляет собой формулу.
Действительно, в первом выражении между высказыванием ![]() и высказыванием ┐
и высказыванием ┐![]() вообще нет никакой логической
связки, поэтому
вообще нет никакой логической
связки, поэтому ![]() ┐
┐![]() не является формулой.
не является формулой.
Для каждой формулы можно построить соответствующую таблицу истинности.
