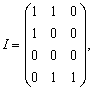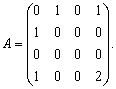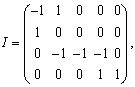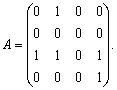Лекция 12. Графы
Ориентированные графы
Определение 4.6. Полустепенью исхода (захода) вершины
графа 
будем
называть число 
(соответственно
), равное количеству
дуг графа, исходящих из вершины (заходящих в вершину ). Вклад каждой петли, инцидентной
вершине , равен
1 как в , так
и в .
Очевидно, что для любого ориентированного псевдографа выполняется равенство:
.
Вершину , для которой 
называют стоком,
а у которой 
- истоком.
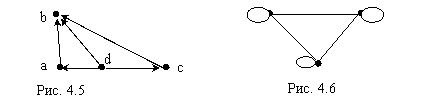На рис. 4.5 показан орграф,
у которого 
, 
, 
, 
,
, 
.
Вершина 
этого графа является стоком, а вершина
- истоком.
Если граф не имеет ребер (т.е. 
),
то все его вершины изолированы, и он называется пустым или нуль-графом.
Простой неориентированный граф, в котором любые две
вершины соединены ребром, называется полным. Полный граф с 
вершинами обозначают символом
(рис.4.2, граф
). Граф порядка
n без ребер называется
пустым и обозначается 
. Граф 
называется тривиальным. Можно расширить
полный граф до полного графа с петлями, добавляя петлю в каждой вершине
(рис.4.6). В ориентированном полном графе имеются пары ребер,
по одному в каждом направлении, соединяющие любые две различные вершины.
Турниром называется орграф, любую пару вершин которого соединяет только одна дуга. Турнир отличается от полного ориентированного графа тем, что у него нет противоположно направленных дуг.
Граф называется однородным (регулярным)
степени 
, если степени всех его вершин одинаковые и
равны . Однородный
граф степени 1 называется паросочетанием. Примерами однородных графов
могут служить графы, образованные вершинами и ребрами пяти первых правильных
многогранников (или, так их называют, платоновых тел): тетраэдра
и куба (степени 3), октаэдра (степени 4), додекаэдра (степени 3), икосаэдра
(степени 5). Граф третьей степени называют кубическим, он обладает рядом
интересных свойств и, в частности, всегда имеет четное число вершин. Три кубических
графа изображены на рис.4.2.
Из выписанной выше формулы, связывающей
число звеньев графа 
со степенями его вершин, для случая однородного
графа степени (все 
), получим:
.
Напоминаем, что 
- число вершин графа. Поэтому, если нечетное число, то 
должно быть четным, и,
следовательно, у любого однородного графа нечетной степени (и кубического тоже)
всегда четное количество вершин.
Орграф называется однородным степени
, если полустепени всех его вершин одинаковые
и равны : 
=
=. В этом случае
.
Здесь, как и раньше, и -
число вершин и дуг графа.
Если множество вершин простого графа 
можно
разбить на два непересекающихся подмножества (доли) 
, 
(
) и при этом не существует ребер, соединяющих
вершины одного и того же подмножества, то такой граф называется двудольным
(иначе - биграфом). Полный двудольный
(у него каждая вершина из соединена с каждой вершиной из ). обозначают символом 
где 
, 
. Граф 
изображен на рис 4.13.
Еще раз напоминаем: любой граф есть совокупность множества вершин и множества ребер, при этом ребра фиксируют имеющиеся взаимозависимости между вершинами. Каждое ребро представляет конкретную пару вершин, между которыми установлена такая взаимосвязь. Игнорируя взаимосвязь между какими-то двумя вершинами, мы тем самым ликвидируем (удаляем) соответствующее ребро. Операция удаления ребер порождает новый граф, с теми же вершинами, но с меньшим числом ребер. Если по каким-то соображениям отпадает необходимость принимать во внимание определенную вершину графа, то ее следует удалить. Операция удаления вершины графа более сложная. Кроме самой вершины необходимо еще удалить и все те ребра графа, которые представляли связи удаленной вершины с другими вершинами графа, т.е. все инцидентные ей ребра.
Граф 
, полученный в результате операций
удаления вершин и (или) ребер графа 
, называется частью (иногда подграфом)
графа . Все
вершины и ребра графа 
являются
одновременно вершинами и ребрами графа : 
. В этом случае говорят, что содержится в . Нуль-граф считается частью каждого графа. Граф будет ориентированным или
неориентированным в зависимости от того, каким является граф
.
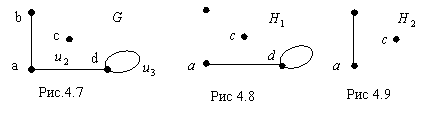
Граф 
, изображенный на рис 4.8,
получен в результате операций удаления ребра графа (этот граф задан на рис. 4.7), а граф 
, показанный на рис. 4.9,
есть результат операций удаления у того же графа вершины .
Пусть 
-
некоторое подмножество множества вершин графа . Часть 
графа называется подграфом,
порожденным (или индуцированным) множеством вершин (вершинно-порожденным
подграфом), если ребрами являются только те ребра множества 
, оба конца которых принадлежат
. Он
получается из графа в
результате удаления всех вершин множества 
и всех ребер, им инцидентных. Для единственной
вершины этот
подграф состоит из самой вершины и из петель вершины , если они имеются.
Подграфом, порожденным множеством
ребер 
(реберно-порожденным подграфом), называют
часть 
графа
, где - некоторое подмножество множества
ребер графа
, а 
есть множество всех вершин графа , которые являются концами
ребер множества .
Такой подграф получается из графа удалением всех ребер множества 
и последующего удаления
всех изолированных вершин получившейся части.
Часть 
графа называется его остовным
подграфом или суграфом. Так как в этом случае 
, то суграф получается из
графа после
удаления некоторых (или даже всех) его ребер.
Замечание. В некоторых работах понятия подграфа и части графа отождествляются,
хотя есть исследователи, занимающиеся теорией графов, которые эти понятия различают,
определяя подграф как часть, полученную в результате операции удаления
у графа некоторых его вершин. Они пользуются только понятиями части, суграфа
и подграфа (в указанном только что смысле). Заметим, что в этом случае любая
часть графа
есть суграф
некоторого подграфа этого графа: вначале у исходного графа удаляем все вершины,
не входящие в часть (вместе
с инцидентными им ребрами), а затем изымаем ребра найденного подграфа, которые
не принадлежат .
Звездный граф
, определяемый вершиной
, состоит из
самой вершины и
всех n вершин графа
ей смежных, а его ребрами
будут все ребра, инцидентные этой вершине.
Для каждой части графа
существует единственная
дополнительная часть графа (дополнение)
, состоящая
из всех ребер ,
которые не являются ребрами , и вершин, инцидентных этим ребрам: 
.
На рис. 4.10
видим граф ,
который есть суграф полного графа 
, и граф -
дополнение графа для
суграфа .
Пусть и -
две части .
Сумма (объединение, наложение) этих частей 
есть часть, состоящая из всех ребер (и вершин,
им инцидентных), которые принадлежат или , или , или им обоим.
Пересечением частей графа и назовем часть графа 
, ребра которой являются ребрами
и одновременно.
Две части и
не пересекаются
по вершинам, если не имеют общих вершин, а следовательно, не имеют и
общих ребер,
и две части не пересекаются
по ребрам, если у них нет общих ребер. Часть и ее дополнение не пересекаются по ребрам,
и 
.
Изоморфизм графов
Ранее было отмечено, что любой абстрактный граф идентичен, или, как говорят математики, изоморфен некоторому геометрическому графу. При изображении геометрических графов имеется большая свобода в размещении вершин и в выборе формы соединяющих их ребер. Поэтому может оказаться, что один и тот же граф представляется различными чертежами, разглядывая которые далеко не сразу можно осознать, что они являются изображениями одного и того же графа. Такие геометрические графы тоже называют изоморфными.
Изоморфизм графов формально определяется следующим образом.
Определение 4.7. Графы 
и
изоморфны, если
существует такое взаимно однозначное соответствие между множествами их вершин
и , что вершины соединены ребрами в
одном из графов в том и только том случае, когда соответствующие им вершины
соединены в другом графе. Если ребра ориентированы, то и их направления также
должны соответствовать друг другу.
Геометрический граф, изоморфный абстрактному графу, называют его геометрической реализацией.
Если графы и изоморфны, то пишут p
(тогда и p). Легко видеть, что отношение изоморфизма
графов рефлексивно, симметрично и транзитивно и является отношением эквивалентности.
Следовательно, множество всех графов разбивается на классы эквивалентности так,
что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Изоморфные графы, как правило, отождествляют, и их можно изображать одним рисунком.
Они могут различаться конкретной природой своих элементов, но именно это и игнорируется
при введении понятия «граф». Нетрудно показать, что три графа, изображенные
на рис. 4.2, изоморфны.
Из определения следует, что изоморфные графы могут различаться лишь обозначениями вершин и ребер, так как у них должно быть равное число вершин и ребер, соответствующие друг другу вершины обязаны иметь одинаковые степени и полустепени, и, разумеется, совершенно все равно, какую геометрическую реализацию графа выбирать для его изображения.
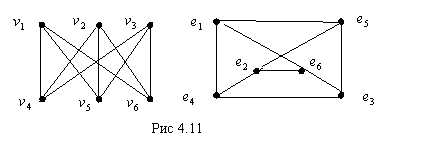
Оба графа на рис. 4.11 изоморфны, так как
существует взаимно однозначное соответствие 
, сохраняющее смежность.
Говорят, что граф изоморфно вкладывается
в граф , если
изоморфен некоторой части
графа .
Замечание. Многие практические задачи приводят к необходимости
распознавания изоморфизма и изоморфного вложения сложных структур, заданных
в виде графов. С содержательной точки зрения изоморфизм графов структур означает
тождественность функционирования самих структур, что допускает в некоторых случаях
замену одной структуры другой, ей изоморфной. Однако для того чтобы выяснить,
изоморфны ли два графа имеющие вершин, в общем случае требуется выполнить
попарных сравнений, а для
распознавания изоморфного вложения графа , имеющего вершин, в граф , у которого вершин, необходимо провести 
сравнений. Поэтому даже
при относительно небольшом количестве элементов в графах (порядка 100) решение
задачи об изоморфизме методом полного перебора практически не реально, необходимо
использовать для этой цели специальные методы.
Вообще говоря, не имеет значения, как нарисовать граф, поскольку все его изображения являются изоморфными графами и несут одну и ту же информацию. Однако встречаются ситуации, когда крайне важно, чтобы изображение графа на плоскости удовлетворяло определенным требованиям. Например, в радиоэлектронике при изготовлении микросхем печатным способом электрические цепи наносятся на поверхность изоляционного материала. А так как проводники не изолированы, то они не должны пересекаться. Аналогичная задача возникает при проектировании железнодорожных и иных путей, где нежелательны переезды.
Определение 4.8. Геометрический граф назовем плоским графом, если он нарисован на плоскости так, что все линии, изображающие его ребра, пересекаются только в точках, соответствующих вершинам графа, т.е. любая точка пересечения таких линий есть вершина, инцидентная ребрам, которые эти линии изображают. Любой граф, изоморфный плоскому графу, называют планарным.
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку). Планарный граф можно уложить на плоскости, а плоский граф - это граф, уже уложенный на плоскости. Плоский граф есть изображение планарного графа, однако не каждое изображение планарного графа является плоским графом.
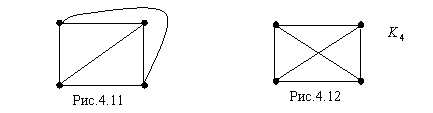
Пример плоского
графа приведен на рис. 4.12. Изоморфный ему полный граф (рис.4.13), укладываемый
на плоскости, имеет два пересекающихся ребра, поэтому граф не является плоским - он только планарный.
На рис 4.13. показаны графы
Понтрягина -
Куратовского,
играющие фундаментальную роль в теории планарности графов. Они не являются планарными
графами. Граф 
представляет собой полный граф наименьшего
порядка, который, не являясь планарным графом (полные графы 
, 
, -
планарные), становится планарным после удаления хотя бы одного его ребра. Второй
(двудольный граф ) является моделью известной задачи о трех
домах и трех колодцах.
.
Для приложений чрезвычайно важно найти и описать необходимые и достаточные условия планарности графов. Следует отметить, что практическая проверка таких условий, как правило, является достаточно сложной задачей. Однако разработаны эффективные алгоритмы, позволяющие для любого заданного графа или найти его плоскую укладку, или установить, что граф не планарен. Достаточно очевидны следующие теоремы.
Теорема 4.2. Любая часть (подграф) планарного графа есть планарный граф.
Теорема 4.3. Плоский граф не должен
иметь в качестве своей части графы Понтрягина - Куратовского.
Для того чтобы сформулировать широко известный
критерий планарности Понтрягина -
Куратовского,
необходимо ввести понятие гомеоморфизма графов. Операция подразбиения ребра
, образованного
парой вершин 
и
, состоит в
удалении ребра и
добавлении двух новых ребер 
и 
, отвечающих парам вершин , и , соответственно. Здесь -
новая (дополнительная) вершина графа. На рис 4.14 показан граф до операции подразбиения
ребра , а на
рис. 4.15 изображен граф, получившийся в результате этой операции.
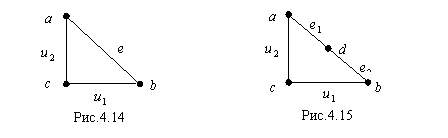
Два графа называются гомеоморфными, если они могут быть получены из одного и того же графа подразбиением его ребер.
Фундаментальное значение в теории планарности имеет
критерий планарности Понтрягина - Куратовского.
Теорема 4.4. Граф планарен тогда и только
тогда, когда он не содержит частей, гомеоморфных графам Понтрягина-Куратовского.
Матричное представление графов
Пусть - помеченный граф, имеющий вершин и ребер. Вершины и ребра помеченного графа пронумерованы.
Пусть 
- вершины графа, а 
-
его ребра. Отношение инцидентности можно определить матрицей 
, имеющей строк и столбцов. Столбцы соответствуют
ребрам графа, а строки - вершинам. Если
неориентированное ребро (звено) 
инцидентно вершине 
, то 
. Когда ориентированное ребро (дуга) 
инцидентно вершине 
, то 
, если вершина -
начало дуги, и 
,
если вершина - конец этой дуги. Если ребро является петлей и вершина
ей инцидентна, то 
,
для орграфа и неографа. Пусть ребро (неважно, что это - звено, дуга или петля) не инцидентно вершине, тогда 
. Матрица, полученная таким
образом, называется матрицей инцидентности графа. Каждый помеченный
граф может иметь только одну матрицу инцидентности, а всякая матрица инцидентности
полностью определяет соответствующий граф.
Матрицей смежности графа
называют квадратную матрицу 
размера 
, строкам и столбцам которой соответствуют
вершины помеченного графа (первый столбец (строка) отвечает первой вершине и
т.д.), а ее элементы находятся по следующим правилам. Для неориентированного
графа 
равно
количеству ребер, инцидентных вершинам с номерами 
и 
. Петле в вершине i соответствует 
. Для ориентированного графа равно количеству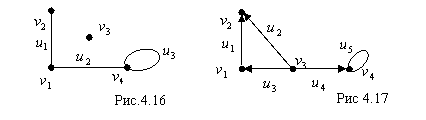 
ребер, выходящих из вершины
и заходящих в вершину 
. Петле в вершине i орграфа соответствует 
.
) и смежности (матрица 
):
)
и смежности (матрица 
):
