Лекция 11. Графы

Геометрические графы

Глава о графах начиналась с рассказа о неких рисунках и схемах, которые Д. Кёниг предложил называть графами. Тем не менее, в предыдущем пункте, где давались определения понятия графа, рисунки или схемы даже не упоминались. Дело в том, что выше речь шла о так называемых абстрактных графах, а рисунки и схемы представляют собой геометрические графы. Эти два понятия хотя и очень близкие, но, тем не менее, различные.

Определение 4.3. Геометрический граф  - это совокупность , где  - непустое множество точек пространства, а  - множество простых кривых (возможно, направленных), удовлетворяющих следующим условиям:

1.      каждая замкнутая кривая множества  содержит только одну точку множества ;

2.      каждая незамкнутая кривая множества  содержит ровно две точки множества , которые являются ее граничными точками;

3.      кривые множества  не имеют общих точек, за исключением точек из множества .

Элементы множества  называют вершинами графа, а само это множество - носителем графа; элементы множества  называются ребрами графа, а само  - его сигнатурой.

            Таким образом, геометрический граф есть просто геометрическая конфигурация или структура в пространстве, состоящая из множества точек, взаимосвязанных множеством простых (не имеющих точек самопересечения) кривых. На рис. 4.1 изображены два  геометрических графа.

            Очевидно, что вершины любого абстрактного графа можно представить точками пространства, а его ребра отождествить с некоторыми простыми кривыми, соединяющими концы этих ребер. Поэтому любой абстрактный граф всегда эквивалентен (по отношению к свойствам, изучаемым в теории графов) некоторому геометрическому графу. Геометрический граф, эквивалентный в указанном выше смысле абстрактному графу, будем называть изображением этого абстрактного графа. Таким образом, геометрические графы можно рассматривать как удобное и наглядное представление абстрактных графов, а не просто как частный случай. Отметим только, что существует огромное количество вариантов расположения вершин геометрического графа в пространстве и не меньшее количество способов начертания его ребер. Следовательно, у абстрактного графа могут быть различные по виду изображения, на первый взгляд совершенно не похожие друг на друга. Оба графа на рис.4.1 являются изображениями абстрактного графа из примера 4.1. Не похожи и три изображения абстрактного графа, показанные на рис. 4.2.

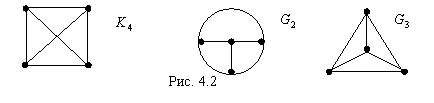
            Кстати, граф  на рис.4.2 представляет собой неориентированный дубликат орграфа (рис. 4.3).

Хотя многие графы, представляющие реальные объекты, являются геометрическими графами, с точки зрения теории графов их единственная структурная особенность состоит в том, что с каждым геометрическим ребром связаны две (возможно, совпадающие) геометрические вершины. Теория графов построена с учетом именно этой особенности и не учитывает реальной природы вершин и ребер. Таким образом, нумерация вершин и ребер с фиксацией вершин концов каждого ребра и указанием его ориентации (в тех случаях, когда это необходимо) содержит всю информацию, достаточную для описания и геометрического графа, и абстрактного графа. Все понятия и определения, введенные выше для абстрактных графов, справедливы и для их изображений, т.е. для геометрических графов.

            Заметим, что введение абстрактного графа позволяет не только избавиться от случайных геометрических характеристик, сохранив наиболее существенные комбинаторные свойства графа. Оно расширяет возможности приложения теории, так как многие реальные структуры имеют комбинаторные свойства, которые удобно рассматривать как граф. Например, в виде графа можно задать соотношения между отдельными работами, которые составляют сложные проекты. В этом случае ребра, после того как задана их ориентация, представляют отдельные работы, а вершины отражают последовательность их выполнения.

Взвешенные графы

Следующий шаг в описании связей между объектами с помощью графов состоит в приписывании ребрам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами. В простейших случаях это может быть порядковая нумерация ребер, указывающая на очередность их рассмотрения (приоритет или иерархия). Вес ребра может означать длину (пути сообщения), пропускную способность (линии связи), напряжение или ток (электрические цепи), количество набранных очков (турниры), валентность связей (химические формулы), количество рядов движения (автомобильные дороги), цвет проводника (монтажные схемы электронного устройства), характер отношения между людьми (сын, отец, подчиненный, учитель) и т. п.

            Вес можно приписывать не только ребрам, но и вершинам. Например, вершины, соответствующие населенным пунктам, могут характеризоваться количеством мест в гостиницах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта – атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.

Определение 4.4. Графы, вершинам и (или) ребрам которых приписаны некоторые веса, называют взвешенными графами. Графы, вершины которых пронумерованы, еще называют помеченными графами.

            Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, называемые графами потоков сигналов или сигнальными графами. Вершины сигнального графа отождествляются с некоторыми переменными, описывающими состояние системы, а вес каждой вершины означает функцию времени или некоторой величины, характеризующую соответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, задающее передачу сигнала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.

Степени вершин

Пусть  - неориентированный граф.

Определение 4.5. Степенью вершины  графа   будем называть число , равное количеству звеньев графа, инцидентных вершине . Вершина графа, имеющая степень 0, называется изолированной, а степень 1 - висячей.

            При подсчете звеньев, инцидентных вершине , некоторую неопределенность вносят петли, так как их можно считать и как единственное, и как двойное звено. В зависимости от рассматриваемой задачи, может оказаться более удобным как тот, так и другой способ подсчета. Чтобы не возникали недоразумения, следует в каждом случае указывать, считается петля однократным звеном или двойным.

            Число , равное числу звеньев, соединяющих вершины  и , назовем кратностью этих вершин. Если у графа нет кратных звеньев, то  или , при этом у неориентированных графов .

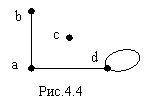
             У графа, представленного на рис. 4.4,  =1 (висячая вершина), =0 (изолированная вершина) и =2, если считать петлю однократным звеном. При этом , а .

Выпишем несколько простых формул. Очевидно, что степень любой вершины графа  равна сумме кратностей всех пар вершин , :

.

            Так как каждое звена графа принимается во внимание при вычислении степеней обоих его концов, то число звеньев графа  связано со степенями и кратностью его вершин соотношением  (лемма о рукопожатии) :

.

Эти формулы справедливы и при наличии у графа петель, если только при подсчете степеней вершин петли считать дважды. Из последней формулы следует, что сумма степеней всех вершин неографа всегда четна, следовательно,

.

Сумма в левой части этой формулы, естественно, останется четной даже в том случае, когда отбрасываются все четные степени вершин. Поэтому справедлива следующая теорема.

Теорема 4.1. В конечном графе число вершин с нечетной степенью всегда четное.

Это утверждение установлено Эйлером и является исторически первой теоремой теории графов.