Лекция 1. Множества.

При изложении теории множеств мы будем придерживаться так называемой интуитивной точки зрения, согласно которой такие понятия, как «множество», «элемент множества», относятся к начальным (примитивным) понятиям математики и поэтому не подлежат определению.

Математическое понятие множества постепенно выделилось из привычных представлений о совокупности, собрании, классе и т.д. Один из создателей теории множеств – Георг Кантор представлял множество как «совокупность или набор определенных и различимых между собой объектов, мыслимых как единое целое».

С понятием множества мы соприкасаемся прежде всего тогда, когда по какой-либо причине объединяем по некоторому признаку в одну группу какие-то объекты и далее рассматриваем эту группу или совокупность как единое целое. Множества принято обозначать заглавными латинскими буквами. Объекты, которые образуют множество, называют элементами множества и для обозначения элементов используют, как правило, малые буквы латинского алфавита. Если a является элементом множества M, то будем говорить, что a принадлежит множеству M, и использовать запись a О M, в противном случае, если a не принадлежит множеству M, будем использовать обозначение a П M.

В различных приложениях дискретной математики чаще всего встречаются конечные множества. Интуитивный смысл этого термина ясен: такие множества содержат конечное число элементов. Число элементов конечного множества называют мощностью этого множества и обозначают символом Card A или |A|.

Наряду с конечными множествами в математике рассматривают и бесконечные множества, то есть такие, которые содержат бесконечно много элементов. Так, например, бесконечно множество натуральных чисел N, множество рациональных чисел Q, множество действительных чисел R.

Способы задания множеств

1. Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы множества записывают внутри фигурных скобок, например: или A={студент А., рабочий Л., школьник М.}.

2. Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись, которую читают следующим образом: «A есть множество элементов b таких, что для них выполняется свойство B». Например, а – четное натуральное число.

3. Множество можно задать порождающей процедурой, например: А={a|a=2k, k-любое натуральное число}.

Наряду с порождающей процедурой существует распознающая или разрешающая процедура, которая позволяет определить, принадлежит ли данный объект множеству или нет. Для множества A={a|b=ka}, k- целое число, распознающая процедура заключается в том, что для любого натурального числа будут проверять, является ли число a делителем числа b. Для множества A распознающая процедура заключается в разложении числа на простые множители.

Пустое и универсальное множества

Определение 1.1. В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом Ж.

В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным (универсумом) и обозначать символом U. Например, при сборке некоторого изделия универсальным множеством естественно назвать множество всех деталей и сборочных элементов, из которых это изделие состоит. Если мы рассматриваем множества, связанные с какими-нибудь фигурами на плоскости, то в качестве универсального множества можно выбрать множество всех точек плоскости.

Определение 1.2. Два множества и называются равными, если они состоят из одних и тех же элементов. Поэтому несуществен порядок записи в фигурных скобках элементов множества, задаваемого списком т.е. {a,b,c,d}={c,b,a,d}.

Операции над множествами

Определение 1.3. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут AМB, где М есть знак вложения подмножества. Из определения следует, что для любого множества справедливы, как минимум, два вложения AМA и AМU.

Определение 1.4. Если AМB и A№B и A№Ж, то A называется собственным подмножеством множества B. В этом случае A содержит хотя бы один элемент, не принадлежащий B.

В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества: Ж№B.

Пустое множество и само множество A называются несобственными подмножествами множества A.

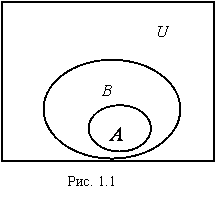
При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника

Определение 1.5. Объединением множеств A и B (обозначение AИB) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2).

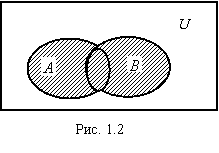
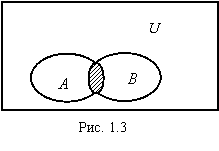
Определение 1.6. Пересечением множеств A и B (обозначение AЗB) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3):

Определение 1.7. Разностью A\B множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4):

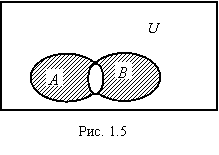
Определение 1.8. Симметрической разностью A/\B множеств A и B называется множество (рис. 1.5).

Определение 1.9. Абсолютным дополнением множества называется множество всех элементов, не принадлежащих A, т.е. множество U\A, где U – универсальное множество (рис. 1.6).

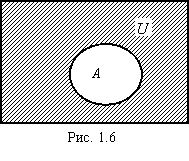
В дальнейшем вместо термина «абсолютное дополнение» мы будем употреблять термин «дополнение».

Свойства операций

Для любых множеств A, B, C выполняются следующие тождества:

1. AИB=BИA, AЗB=BЗA (коммутативность объединения и пересечения);

2. (AИB)ИC= AИ(BИC), (AЗB)ЗC= AЗ(BЗC) (ассоциативность объединения и пересечения);

3. AЗ(BИC)= (AИB)З (AИC), AИ(BЗC)= (AЗB)И (AЗC), (дистрибутивность пересечения относительно объединения и объединения относительно пересечения);

4. AИA=A, AЗA=A, (идемпотентность объединения и пересечения);

5. AИU=U, AЗU=A, AИЖ=A, AЗЖ=Ж, AИ`A=U, AЗ`A=Ж (свойства универсального и пустого множеств);

6. щщA=A (закон двойного дополнения),
Знак щ используется для операции отрицания или дополнения наряду с чертой сверху;

7. щ(AИB)= щA З щB
щ(AЗB)= щA И щB (законы де Моргана) .